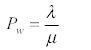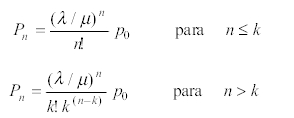Las colas o lineas de espera son un aspecto de nuestras vidas que nos encontramos continuamente en nuestras actividades diarias como lo es un Banco, Cajeros automáticos, Elevadores, Super mercados, etc.
El origen de la Teoría de Colas está en el esfuerzo de Agner Kraup Erlang (Dinamarca, 1878 - 1929) en 1909 para analizar la congestión de tráfico telefónico con el objetivo de cumplir la demanda incierta de servicios en el sistema telefónico de Copenhague. Sus investigaciones acabaron en una nueva teoría denominada teoría de colas o de líneas de espera.
2.1 Agner Krarup Erlang
Biografía
Erlang aprobó con distinción el examen de ingreso para la Universidad de Copenhague en 1896. Obtuvo una beca para la universidad y se graduó en matemáticas en 1901. Durante los siguientes años sería profesor, pero mantuvo su interés en las matemáticas y recibió un premio por un artículo que remitió a la Universidad de Copenhague.
Fue miembro de la asociación danesa de matemáticas, por medio de la cual conoció a Johan Jensen, el ingeniero jefe de la Copenhagen Telephone Company (CTC), la cual era una subsidiaria de International Bell Telephone Company. Erlang trabajó por casi 20 años para CTC, desde 1908 hasta su muerte en Copenhague en 1928.
Contribuciones
Mientras trabajó para la CTC, a Erlang se le presentó el problema clásico de la determinación de cuántos circuitos eran necesarios para proveer un servicio telefónico aceptable.
Erlang puso manos a la obra investigando directamente el problema. El realizó medidas en terreno y era un experto en la historia y el cálculo de las tablas numéricas de algunas funciones matemáticas, particularmente logarítmicas.
Erlang desarrolló su teoría del tráfico telefónico a través de varios años. Entre sus publicaciones más importantes sobre la materia, se encuentran:
- En 1909 - "La teoría de las probabilidades y las conversaciones telefónicas"1 - la cual demostró que la Distribución de Poisson se aplica para tráfico telefónico aleatorio.
- En 1917 - "Solución de algunos problemas en la teoría de probabilidades de importancia en centrales telefónicas automáticas"2 - el cual contiene su fórmula clásica para el cálculo de pérdidas y tiempos de espera.
Un compendio de sus trabajos fue publicado posteriormente por la Copenhaguen Telephone Company en 1.9483
El interés por su trabajo continuó después de su muerte y hacia 1944 el "Erlang" era usado en los países escandinavos para denotar la unidad de tráfico telefónico. Esta unidad de medida fue reconocida internacionalmente al final de la segunda guerra mundial4
También una distribución estadística y un lenguaje de programación (listados abajo), han sido nombrados en su honor.
2.2 Distribución exponencial
La distribución exponencial es el equivalente continuo de la distribución geométrica discreta. Esta ley de distribución describe procesos en los que:
- Nos interesa saber el tiempo hasta que ocurre determinado evento, sabiendo que,
- el tiempo que pueda ocurrir desde cualquier instante dado t, hasta que ello ocurra en un instante tf, no depende del tiempo transcurrido anteriormente en el que no ha pasado nada.
Ejemplos de este tipo de distribuciones son:
- El tiempo que tarda una partícula radiactiva en desintegrarse. El conocimiento de la ley que sigue este evento se utiliza en Ciencia para, por ejemplo, la datación de fósiles o cualquier materia orgánica mediante la técnica del carbono 14, C14;
- El tiempo que puede transcurrir en un servicio de urgencias, para la llegada de un paciente;
- En un proceso de Poisson donde se repite sucesivamente un experimento a intervalos de tiempo iguales, el tiempo que transcurre entre la ocurrencia de dos sucesos consecutivos sigue un modelo probabilístico exponencial. Por ejemplo, el tiempo que transcurre entre que sufrimos dos veces una herida importante.
La distribución exponencial es una distribución de probabilidad continua con un parámetro λ > 0 cuya función de densidad es:
Su función de distribución es:
Donde e representa el número e.
El valor esperado y la varianza de una variable aleatoria X con distribución exponencial son:
Función de densidad de probabilidad
FUENTE: http://www.bioestadistica.uma.es/libro/node78.htm
2.3 Distribución poisson
La Distribución de Poisson se llama así en honor a Simeón Dennis Poisson (1781-1840), francés que desarrolló esta distribución basándose en estudios efectuados en la última parte de su vida.
La distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad que ocurra un determinado número de eventos durante cierto periodo de tiempo.
Por ejemplo: La distribución de las llamadas telefónicas que llagan a un conmutador, la demanda (necesidades) de servicios en una institución asistencial por parte de los pacientes, los arribos de los camiones y automóviles a la caseta de cobro y el número de accidentes en un cruce. Los ejemplos citados tienen un elemento en común, pueden ser descritos por una variable aleatoria discreta que asume valores enteros (0,1,2,3,4,5 y así sucesivamente)
La función de masa de la distribución de Poisson es:
donde
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
- e es la base de los logaritmos naturales (e = 2,71828 ...)
2.4 Teoria de colas o líneas de espera
Teoria = Conjunto de principios interconectados para que un sistema opere o funcione.
La teoría de colas es el estudio matemático del comportamiento de líneas de espera. Esta se presenta, cuando los "clientes" llegan a un "lugar" demandando un servicio a un "servidor", el cual tiene una cierta capacidad de atención. Si el servidor no está disponible inmediatamente y el cliente decide esperar, entonces se forma la línea de espera.
Una cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de línea de espera particulares o sistemas de colas. Los modelos sirven para encontrar un buen compromiso entre costes del sistema y los tiempos promedio de la línea de espera para un sistema dado.
Los sistemas de colas son modelos de sistemas que proporcionan servicio. Como modelo, pueden representar cualquier sistema en donde los trabajos o clientes llegan buscando un servicio de algún tipo y salen después de que dicho servicio haya sido atendido. Podemos modelar los sistemas de este tipo tanto como colas sencillas o como un sistema de colas interconectadas formando una red de colas. En la siguiente figura podemos ver un ejemplo de modelo de colas sencillo. Este modelo puede usarse para representar una situación típica en la cual los clientes llegan, esperan si los servidores están ocupados, son servidos por un servidor disponible y se marchan cuando se obtiene el servicio requerido.
El problema es determinar qué capacidad o tasa de servicio proporciona el balance correcto. Esto no es sencillo, ya que un cliente no llega a un horario fijo, es decir, no se sabe con exactitud en que momento llegarán los clientes. También el tiempo de servicio no tiene un horario fijo.
2.4.1 Elementos que conforman el sistema de colas:
· Poblacion (entidades): Elemento que tiene la característica de la población.
· Sistema de cola (distribución poisson)
· Sistema de servidores, ventanilleros (distribución exponencial)
IMPORTANTE: La condicion para que haya cola es que el numero de entidades debe ser mayor que el numero de servidores.
2.4.2 Nomenclatura para la clasificación de un sistema de colas
S : Número de servidores
n : Número de clientes en el sistema
N: Número máximo de clientes permitidos en el sistema
A,,t: Flujo de clientes que entran cuando hay n clientes en el sistema
u,7l: Capacidad del servidor cuando hay n clientes en el sistema.
E(t): Tiempo promedio de proceso por cliente
V(t): Variancia del tiempo de proceso
E(á): Tiempo promedio entre llegadas
V(a): Variancia del tiempo entre llegadas
CQ: Coeficiente cuadrado de variación del flujo de clientes que entran al
sistema
C2S: Coeficiente cuadrado de variación del tiempo de servicio
Cp: Coeficiente cuadrado de variación del flujo de clientes que salen del
sistema PIJ: Probabilidad de que el sistema cambie de un estado i a un estado y
después de un intervalo de tiempo
Pn: Probabilidad en estado estable de que existan n clientes en el sistema
L: Número promedio de clientes en el sistema
Lq: Número promedio de clientes en la fila
W: Tiempo promedio de permanencia en el sistema
Wq: Tiempo promedio de permanencia en la fila
P: Utilización promedio del servicio
Ct: Costo total promedio del sistema de líneas de espera por unidad de
tiempo
Ce: Costo promedio de servicio por cliente por unidad de tiempo
Cq: Costo promedio de espera por cliente por unidad de tiempo
2.4.3 Clasificación de kendall - Lee
En 1953 Kendall y Lee propusieron un sistema de clasificación de los sistemas de líneas de
espera, ampliamente utilizado en la actualidad. Esta clasificación considera seis de las
características mencionadas en la estructura de los modelos de líneas de espera,
expresándolas en el formato (a / b I c) (d I e I f), donde:
a distribución de probabilidad del tiempo entre llegadas de las
transacciones. b distribución de probabilidad del tiempo de servicio.
Los símbolos utilizados en estos dos primeros campos son:
D: constante.
Ek: distribución Erlang con parámetro k.
G: cualquier tipo de distribución.
GI: distribución general independiente.
H: distribución hiperexponencial.
M : distribución exponencial. c número de servidores d orden de atención a los
clientes.
Los símbolos utilizados en este campo son:
FCFS: primeras entradas, primeros servicios.
LCFS: últimas entradas, primeros servicios
SIRÓ: orden aleatorio.
PR: con base en prioridades.
GD: en forma general.
e: Número máximo de clientes que soporta el sistema en un mismo instante de tiempo.
/: Número de clientes potenciales del sistema de líneas de espera.
2.4.4 Modelos de líneas de espera de un solo canal. (M/M/1)
Suposiciones:
· La línea de espera tiene 1 solo canal
· Patrón de llegadas con distribución poisson
· Tiempo de servicio con distribución exponencial
· Disciplina del servicio FIFO
Las fórmulas que se emplean para determinar las características de operación del estado estable son:
λ= Número promedio de llegadas por periodo (tasa promedio de llegadas)
µ= Número promedio de servicios por periodo ( tasa promedio de servicio)
- Probabilidad de que no haya unidades en el sistema
· Número promedio de unidades en la fila de espera (tamaño de la fila)
· Número promedio de unidades en el sistema (tamaño total)
· Tiempo de espera promedio que una unidad pasa en la línea de espera
· Tiempo promedio que una unidad pasa en el sistema
· Probabilidad de que una unidad que llega tenga que esperar para obtener servicio
· Probabilidad de que hayan n unidades en el sistema.
Donde λ/µ = factor de utilización del servicio. Este proporciona la probabilidad de que la instalación de servicio este ocupada.
Estas formulas del 1 al 7 solo se aplican cuando
µ> λ;
esto es, la tasa promedio de servicio > tasa promedio de llegadas;
o sea, cuando λ/µ < 1 ; en caso contrario la cola crece sin limite, pues el servicio no tiene capacidad para manejar las unidades que llegan.
Ejercicio propuesto:
Suponga que un cajero bancario puede atender a los clientes a una velocidad promedio de diez clientes por hora (m = 10). Además, suponga que los clientes llegan a la ventanilla del cajero a una tasa promedio de 7 por hora (l= 7). Se considera que las llegadas siguen la distribución exponencial. En la condición uniforme el sistema de colas tendrá las siguientes características de desempeño.
r = 7 / 10, el prestador del servicio trabajara el 70% del tiempo.
P0 = 1- 7 / 10 = 0.3; 30% del tiempo no habrá clientes en el sistema ( ni en la cola, ni recibiendo servicio).
Pn = 0.3 ( 7 / 10 )n, una formula para descubrir la posibilidad de que n se encuentre en el sistema en cualquier momento dado: n = 1,2,3,.......; P1 = 0.21, P2 = 0.147; P3 = 0.1029; etc.
Lq = 72 = 1.63; en promedio 1.63 clientes estarán en la cola.
Ls = 7 / ( 10 - 7 ) = 2.33; en promedio 2.33 clientes estarán en el sistema (en la cola y en servicio)
Wq = 7 = 0.233; el cliente pasa un promedio de 0.233 horas esperando en la cola.
Ws = 1 / ( 10 - 7 ) = 0.333; el cliente pasa un promedio de 0.333 horas en el sistema (en la cola en servicio).
Si los clientes se alejan del cajero siempre que existan 3 o más clientes antes que ellos en el sistema, la proporción de clientes perdida es:
1- (P0 - P1 - P2 - P3 ) = 1- ( 0.3 - 0.21 - 0.147 - 0.1029 ) = 0.2401
En este caso se perderá el 24% de los clientes debido a que la espera es demasiado larga.
Ahora es posible evaluar el desempeño del sistema de colas. El administrador tendrá que tomar en consideración el tiempo perdido del prestador del servicio ( 30% ), el tiempo que espera el cliente ( 0.233 horas ) y la longitud de la línea que se forma ( 1.63 clientes). Si este rendimiento es inaceptable se puede colocar un segundo prestador del servicio o hacer otros cambios en las características de las llegadas, de la cola o del portador de los servicios.
2.4.5 Modelos de líneas de espera de canales múltiples. (M/M/K)
Suposiciones
· la línea de espera tiene 2 ó más canales (instalaciones de servicio).
· el patrón de llegada es de distribución de poisson.
· el tiempo de servicio de cada canal sigue una distribución exponencial.
· la tasa promedio de servicioµ , es la misma para todos los canales.
· Las unidades que llegan aguardan en una sola linea de espera y después pasan al primer canal libre para obtener servicio.
· La disciplina del servicio es FIFO.
Caracteristicas de operación
λ= tasa promedio de llegadas al sistema
µ= tasa promedio de servicio para cada canal
k = número de canales
kµ= tasa promedio de servicio para el sistema de canales múltiples
La condición de aplicabilidad de las formulas que siguen es:
kµ>λ
- Probabilidad de que no haya unidades en el sistema
- Número promedio de unidades en la fila de espera (tamaño de la fila
- Número promedio de unidades en el sistema (tamaño total)
· Probabilidad de que una unidad que llega tenga que esperar para obtener servicio
· Probabilidad de que haya n unidades en el sistema.
· Ejercicios y ejemplos
· Video de teoría de colas (youtube)
2.4.6 Ecuaciones de flujo de Little
Las principales características de operación que interesan en las líneas de espera son:
El número promedio de unidades en la línea de espera, el número de unidades en el sistema, el tiempo promedio que cada unidad pasa en la línea de espera y el tiempo promedio que cada unidad pasa en el sistema, esto es:
John D.C. Little muestra que estas cuatro características están relacionadas en forma general y se aplican a diversos modelos de líneas de espera, independientemente.
Una ecuación general es:
Una ecuación general es:
Igualmente,
de donde :
Otra, ecuación general es:
De donde:
La importancia de las ecuaciones de Little es que se aplican a cualquier modelo de espera independientemente de si las llegadas siguen una distribución poisson o no y si los tiempos de servicio siguen una distribución exponencial o no.
· Ejercicios y ejemplos
FUENTE: